Nom

III. ENGRENAGES DROITS (OU PARALLÈLES) À DENTURE DROITE

PJ

Engrenages typiques : pignon/roue, pignon/couronne intérieure et pignon crémaillère. Le pignon est la plus petite des deux roues (c'est en général la roue menante ou motrice, celle qui transmet son énergie). La forme des roues varie avec les dimensions.

Figure 4

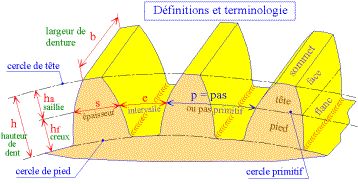
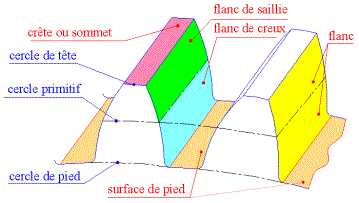
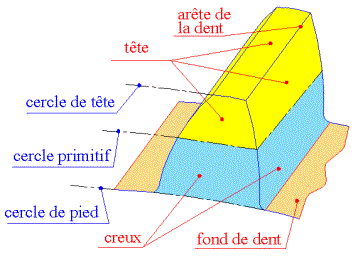
1. Définitions - terminologie et principaux symboles normalisés (NF ISO 701)

Figure 27	Figure 28
Figure 29	Figure 30

Figure 31	Figure 32
Figure 33	Figure 34

CINEMATIQUE CINEMATIQUE

Indices ou signes additionnels* Tableau 1
Indice ou signe	Terme ou observation
1	relatif au pignon
2	relatif à la roue
a	de tête
f	de pied
n	réel
t	apparent
x	axial
r	radial
t	tangentiel
b	de base
f	d'approche
a	de retraite
* symboles à ajouter, si nécessaire, aux symboles principaux.

Principales caractéristiques des engrenages droits (ou parallèles) à denture droite
Caractéristique ou terme	Symbole normalisé (NF ISO701)*	Définitions - observations - formules
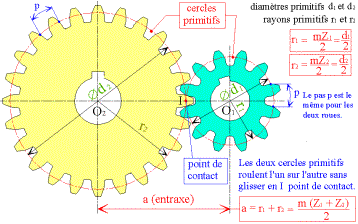
entraxe	a	a = r1+r2 = (d1+d2) = m(Z1+Z2)
largeur de denture	b	b = km (avec 7 k 12)
vitesse angulaire		en rad.s^-1 ; = N/30
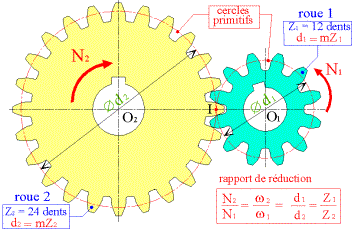
nombre de tours	n	n en tours par minute ou tr.min^-1
vitesse linéaire	v	en m.s^-1 ou autres unités
nombre de dents	Z	Z1 (roue1) et Z2 (roue 2)
module	m	nombre normalisés; voir tableaux des valeurs
pas (pas primitif)	p	p = m (remarque p1 = p2 = p)
rayon primitif	r	r1= mZ1 = d1 ; r2= mZ2 = d2
diamètre primitif	d	d1= mZ1 ; d2= mZ2
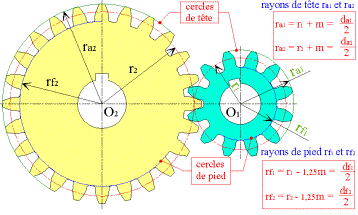
rayon de tête	ra	ra = r + m = r + ha = da
diamètre de tête	da	da = d + 2m = d + 2ha
rayon de pied	rf	rf = r -1,25m= r - hf = df
diamètre de pied	df	df = d -2,5m = d - 2hf
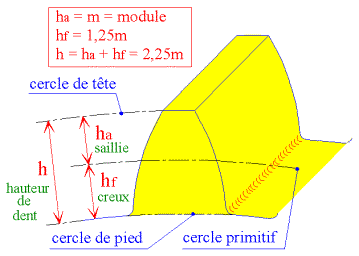
saillie	ha	ha = m
creux	hf	hf = 1,25m
hauteur de dent	h	h = 2,25m = ha + hf
épaisseur de la dent	s	s1 = e1 =s2 =e2 = m (si jeu nul...)
intervalle	e	s1 + e1 = s2 + e2 = p
angle de pression		valeur usuelle: = 20°
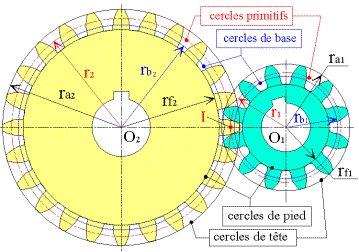
rayon de base	rb	rb = r.cos = db
diamètre de base	db	db = d.cos
pas de base	pb	pb = p.cos
longueur de conduite	g	g = ga + gf
longueur de retraite	ga
longueur d'approche	gf
rapport de conduite		= g/pb
* la norme prévoit les lettres sous forme italique

Figure 35

Circonférence primitive La circonférence primitive, de périmètre d, doit impérativement comporter un nombre entier de dents (Z) toutes placées à intervalles successifs égaux au pas primitif (p). Il en résulte que :.d = p.Z = périmètre circonférence primitive par définition (normalisée ISO...) du module m : m = pas/

l'expression précédente se simplifie et devient :d=m.Z

Pas primitif (p) Sur le cercle primitif, il mesure la distance (la longueur de l'arc primitif) entre les profils homologues de deux dents consécutives.

Autrement dit, le pas est égal à la circonférence primitive (.d) divisée par le nombre de dents Z.

En remarquant que .d = .(mZ) :

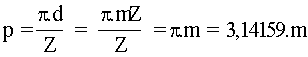
Remarque : les pays anglo-saxons utilisent la notion de "Diamétral pitch P = /pas en pouce".

Module (m)

C'est un nombre dont les valeurs possibles sont normalisées (normes ISO, voir tableau).

Remarque : quel que soit le nombre de dents, toutes les roues de même module et de même angle de pression () peuvent être fabriquées à partir du même outil de taillage.

C'est pour limiter le nombre des outils et des systèmes de mesure qu'une série de modules a été normalisée.

L'épaisseur de la dent et sa résistance dépendent du choix du module. Ce choix ne doit pas être improvisé mais étudié et calculé.

Valeurs normalisées du module (NF ISO 54...) Tableau 3
Valeurs principales en mm	Valeurs secondaires en mm
0,06 - 0,08 - 0,10 - 0,12 - 0,15 0,20 -0,25 -0,30 -0,40 -0,50 -0,75 -1,00 -1,25 -1,50 - 2 -2,5-3 -4 -5 -6 -8 -10 -12 -16 -20 -25 - 32 - 40 - 50 - 600,07 -0,09 -0,11 -0,14 -0,18 - 0,22 - 0,28 - 0,35 - 0,45 - 0,55 - 0,7 - 0,9 - 1,125 - 1,.375 - 1,75 - 2,25 - 2,75 - 3,5 -4,5 - 5,5 - 7 - 9 - 11 - 14 - 18 - 22 -28 -36 -45 -55 -70

Entraxe (a) : c'est la plus courte distance entre les axes d'un engrenage, dans le cas d'un engrenage droit à denture droite cette distance vaut :

a = r₁+r₂ = (d₁+d₂) = m(Z₁+Z₂)