Cinématique Graphique

1. Equiprojectivité des vecteurs vitesses

1.1. Enoncé

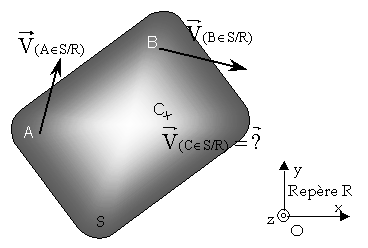
Soient deux points A et B appartenant à un même solide S et et les vecteurs vitesses des points A et B, appartenant à S, par rapport à un même référentiel R. La projection orthogonale de sur est égale à la projection orthogonale de sur . Concrètement :

1.2. Exploitation du théorème de l’équiprojectivité des vecteurs vitesses

Pour pouvoir appliquer ce théorème et réaliser les différentes constructions, nous devons connaître une vitesse intégralement, et connaître, au minimum, le support du vecteur vitesse que nous souhaitons déterminer.

1.3. Détermination d’une vitesse par double équiprojectivité

Soient :

· et deux vitesses connues ;

· une vitesse de direction, de sens et d’intensité inconnue.

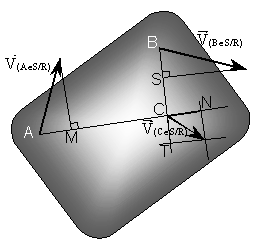
La détermination de est possible par double équiprojectivité à partir des deux vitesses et intégralement connues (direction + sens + intensité).

Remarque : si C était aligné avec A et B, il aurait fallu déterminer la vitesse d’un point D non aligné avec A et B.

2. Centre instantané de rotation

2.1. Définition

Pour tout solide S en mouvement plan par rapport à un repère R, il existe un point I et un seul, ayant une vitesse nulle () à l’instant t considéré et appelé centre instantané de rotation ou CIR.

Le CIR possède les propriétés d’un centre de rotation à l’instant (t) considéré. A l’instant suivant (t’=t+Dt), il y a de fortes chances pour que le CIR ait changé de position.

2.2. Détermination et construction du CIR

En tant que centre de rotation, le CIR est situé à l’intersection des perpendiculaires aux supports des vecteurs vitesses du solide.

2.3. Détermination des vecteurs vitesses grâce au CIR

Puisque I est le Centre Instantané de Rotation, nous pouvons en déduire que: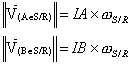

En divisant membre à membre, chaque terme des équations, nous obtenons :

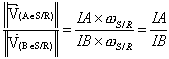Soit Finalement :

Grâce à cette relations, nous sommes capable de déterminer la norme d’une des vitesses inconnues.

2.4. Le CIR et les Mouvements Particuliers

Lorsqu’une pièce subit un mouvement de translation, le CIR est rejeté à « l’infini ». De toute façon, il n’y pas de quoi s’affoler, car dans une mouvement de translation tous les points ont la même vitesse.

Lorsqu’une pièce subit un mouvement de rotation, le CIR se confond avec le Centre de Rotation. C’est une évidence, mais cette remarque dépanne souvent…

Vos commentaires:

3. Composition des vecteurs vitesse

3.1. Vitesses linéaires

Soit un cascadeur 2 marchant sur un camion 1 en mouvement par rapport au sol 0.

La vitesse relative du cascadeur par rapport au camion est _V_2/1.

La vitesse absolue du cascadeur par rapport au sol est _V_2/0, avec _V_2/0 = _V_2/1 + _V_1/0

Cette relation est généralisable à n’importe quels solides S₁ et S₂, par rapport à un référentiel S₀  ou par rapport à un autre solide S_i. Nous en déduisons

Relation de Composition des vecteurs vitesses :

Remarque : Cette relation est générale et reste valable même si les vecteurs vitesses ne sont pas colinéaires.

3.2. Vitesses angulaires

La relation précédente peut être étendue aux vecteurs vitesses angulaires : _W_2/0 = _W_2/1 + _W_1/0

Vos Commentaires :