|
NOM : |
LES BOITES DE VITESSES MECANIQUES |
Page 1 |
LES EFFORTS RéSISTANTS
LA RESISTANCE DUE AU ROULEMENT
C'est la force nécessaire pour entretenir le
déplacement d'un engin roulant sur
un type de sol donné, cette force s'oppose au
déplacement.
FIG 5
La déformation du sol dépend de sa nature: le
pneumatique s'enfonce jusqu'à ce
qu'il atteigne une couche plus compacte capable de
lui résister.
On peut évaluer cette force grâce à un dynamomètre en
tirant l'engin pour entretenir son avancement sur un terrain donné, la force
lue correspondra à la résistance due au roulement dans les conditions précises
du moment.
La force engendrée par la résistance au roulement
peut avoir de nombreuses origines parmi lesquelles le frottement des moyeux, la
géométrie du train avant, le couple de traînée du dispositif de freinage ou des
éléments de transmission entraînés.
On néglige généralement ces efforts pour privilégier
ceux qui sont engendrés par
le pneumatique au niveau de la roue avec le sol, car
ils sont prépondérants.
Pour un engin agricole, la déformation du pneumatique
et du sol constitue un
obstacle perpétuellement renouvelé qui s'oppose de
façon significative à son
déplacement.
La déformation du pneumatique et du sol crée un
écrasement tel que la surface
de contact engendrée, multipliée par la pression
régnant dans le pneumatique, crée une
force capable de compenser le poids supporté par la
roue.
La déformation du pneumatique dépend essentiellement
de sa pression de gonflage et du poids qu'il supporte, mais également du
type de pneumatique (à carcasse diagonale ou radiale).
La masse d'un engin est caractérisée par la quantité
de matière qui le constitue.
la masse s'exprime en kg (ou bien en tonnes
lorsque l'engin est très lourd).1tonne=1000kg
La masse d'un corps est soumise à l'attraction
terrestre elle est attirée vers la
terre par une force. Cette force caractérise le poids
de l'engin, multipliée par le
coefficient de résistance au roulement elle permet de
déterminer la force qui s'oppose à
son déplacement.
LA RESISTANCE DUE AU ROULEMENT
C'est la force nécessaire pour entretenir le
déplacement d'un engin roulant sur
un type de sol donné, cette force s'oppose au
déplacement.
FIG 6
On peut évaluer cette force grâce à un dynamomètre en
tirant l'engin pour entretenir son avancement sur un terrain donné, la force
lue correspondra à la résistance due au roulement dans les conditions précises
du moment.
La force engendrée par la résistance au roulement
peut avoir de nombreuses origines parmi lesquelles le frottement des moyeux, la
géométrie du train avant, le couple de traînée du dispositif de freinage ou des
éléments de transmission entraînés.
On néglige généralement ces efforts pour privilégier
ceux qui sont engendrés par le pneumatique au niveau de la roue avec le sol,
car ils sont prépondérants.
Pour un engin agricole, la déformation du pneumatique
et du sol constitue un obstacle perpétuellement renouvelé qui s'oppose de façon
significative à son déplacement.
La déformation du pneumatique et du sol crée un
écrasement tel que la surface
de contact engendrée, multipliée par la pression
régnant dans le pneumatique, crée une
force capable de compenser le poids supporté par la
roue.
La déformation du sol dépend de sa nature: le
pneumatique s'enfonce jusqu'à ce
qu'il atteigne une couche plus compacte capable de
lui résister.
La déformation du pneumatique dépend essentiellement
de sa pression de
gonflage et du poids qu'il supporte, mais également
du type de pneumatique (à carcasse
diagonale ou radiale).
La masse d'un engin est caractérisée par la quantité
de matière qui le constitue.
la masse s'exprime en kg (ou bien en tonnes lorsque
l'engin est très lourd).
Le poids de cette masse n’est pas la
même dans tous les points du globe puisque la valeur « g » du
coefficient de la pesanteur n’y est pas identique :
G=9,78N/kg à l’équateur
G=9,78N/kg aux pôles
Coefficient de ressitance au roulement
d/r ,
sur macadam : 0,02 à 0,025
sur terrain agricole : 0,14 à 0,25
tracteur à chenilles sur terrain
agricole : 0,07 à 0,12
roue acier sur rail : 0,001 à
0,002
La masse d'un corps est soumise à l'attraction
terrestre elle est attirée vers la
terre par une force. Cette force caractérise le poids de l'engin, multipliée par le coefficient de résistance au roulement elle permet de déterminer la force qui s'oppose à
son déplacement.
La force qui s'oppose au roulement sera d'autant plus grande que:
‑"d" est grand : cette distance est fonction de l'écrasement
du pneu et de son enfoncement dans le sol.
‑'r' est petit : plus le diamètre de la roue est faible et plus le
rapport d/r est grand.
'P' est important : c'est à
dire la charge supportée par l'essieu.
La largeur du pneu ou le jumelage diminue l'enfoncement par augmentation de la surface de contact avec le sol, ce qui limite « d » donc Frr (force due à la résistance au roulement).
La
résistance au roulement c'est l'effort que vous devez exercer pour pouvoir, par
exemple, pousser votre voiture pour la déplacer. Dans votre garage vous y
parviendrez d'autant plus facilement que vos pneus seront bien gonflés!
La résistance au roulement d'un train est
faible puisque ni la roue ni le rail ne se déforment.
(p) force exercée par la masse de l'engin sur le sol
Frr = _____d______ x p
r
(r) coefficient de roulement image de la déformation du pneu et du sol
LA RESISTANCE DUE
A LA PENTE
La force nécessaire pour qu'un engin puisse franchir
une pente est fonction de
son poids et de l'importance de la déclivité.
FIG 7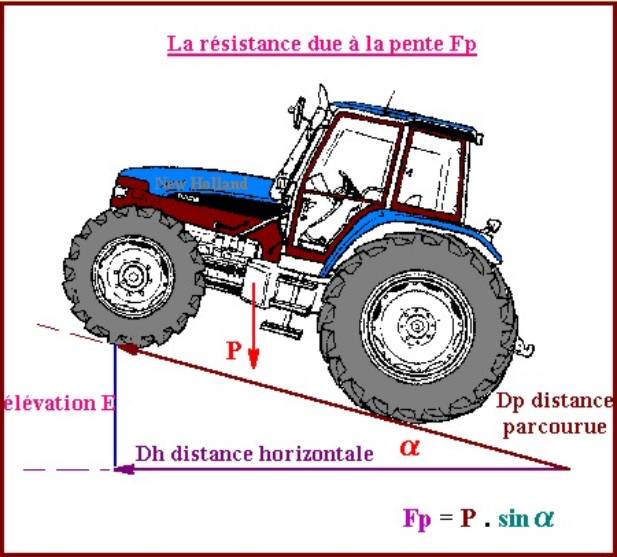
La pente est généralement donnée en pourcentage, elle
exprime l'élévation qui est
mesurée en fonction de la distance horizontale
parcourue.
Par exemple:
si l'élévation est de 5 mètres et la distance
parcourue de 100 mètres, alors:
5:100 x 100 = 5%
La masse (m) s'exprime en kilogramme
Le poids (P) s'exprime en Newton
Pour simplifier les calculs, on
considère g = 10 N/kg
on calcule P avec la relation:
P (N) = m (kg) . g (10N/kg)
L'effort nécessaire pour franchir une pente est
obtenu en multipliant le poids de l'engin par le sinus de l'angle de la pente.
Plus l'engin est lourd, plus la pente est importante
et plus la force nécessaire pour le déplacer sera grande.
La pente, lorsque l'on monte, constitue une force qui
s'oppose au déplacement, à
l'inverse, en descente, elle s'ajoute à l'effort de
traction pour favoriser le déplacement de
l'outil.
La pente = __élévation________
Distance horizontale
La pente = __E_ = tg a
Dh
L’angle
étant généralement très faible
On admet
tg a = sin a
La pente = __distance parcourue_= Dp_
Elévation E
On en déduit l’effort du à la pente :
Fp –P . sin a
Pente Angle Tangente Sinus
en % a a
10 5° 40' 0,10
0,10
15 8° 35' 0,148
0,15
20 11° 18, 0,196
0,20
25 14° 05' 0,242
0,25
30 16° 42' 0,288
0,30
50 26° 35' 0,447
0,50
80 38° 40' 0,625
0,80
100 45° 0,7
1
LA RESISTANCE DUE A L'EFFORT DE TRACTION
Conçu pour remplacer la traction animale, à l'origine
la vocation du tracteur a
consisté, comme son nom l'indique, à engendrer un
effort de traction dans le seul but de
tirer des outils de travail.
FIG 8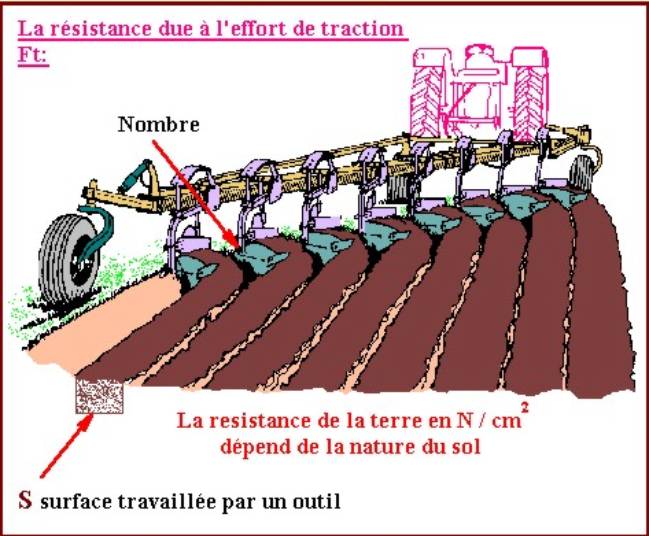
La force de traction peut s'exercer au niveau du
crochet d'attelage dans le cas d'outils traînés (remorquage) , ou bien par
l'intermédiaire de l'attelage trois points lorsqu'il s'agit d'outils
semi-portés essentiellement destinés au travail du sol.
Il est possible de déterminer approximativement par
calcul l'effort engendré par
un outil en fonction de la surface de la bande de
terre découpée.
Ainsi dans le cas classique du labour, la surface de
la terre découpée multipliée par l'effort de coupe -fonction de la nature du
terrain- donne l'effort de traction théorique dû à l'outil.
Voici quelques exemples de valeurs de résistance de
la terre:
terre légère: 3 à 5 N/cm 2
terre très argileuse: 7 à 8 N/cm 2
terre très dure: 8 à 10 N/cm 2
Pratiquement tous les engins sont destinés à
engendrer un effort de traction, c'est le plus souvent leur vocation première.
LA RESISTANCE DUE A L'INERTIE
Elle se caractérise par une force due à la masse de
l'engin et par une force résistante issue de toutes les masses tournantes:
moteur et transmission jusqu'aux roues.
FIG 9
Dans le cas d'un véhicule, l'inertie due aux masses
tournantes est généralement négligée.
Elle est à considérer dans le cas d'un tracteur qui
est doté d'importants rapports de démultiplication, notamment pour les vitesses
très lentes.
Cette inertie due aux masses tournantes est prise en
considération au moyen d'un coefficient qui s'exprime en fonction de la masse
de l'engin.
Fi = g. P/g . km
g
= accélération en m/s2
p/g = masse en kg
km = valeur du coefficient: 1 à 1,3
environ
Ce coefficient représente l'augmentation équivalente
de la masse de l'engin due à
l'inertie des masses tournantes.
Ce coefficient ne représente toutefois que quelques
pour-cents de la force d'inertie totale.
Fi = g. P/g . km
g
= accélération en m/s2
p/g
= masse en kg
km
= valeur du coefficient: 1 à 1,3 environ
Fi : Force d’inertie
g(g) :accéleration
P/g :masse de l’engin
Km : Coefficient représentation les masses
tournantes.
LA RESISTANCE AERODYNAMIQUE
La résistance due à la pénétration dans l'air est
fonction du carré de la vitesse, son influence est extrêmement importante pour
un véhicule routier, elle est presque totalement négligeable pour un engin
agricole ou de travaux publics.
FIG 10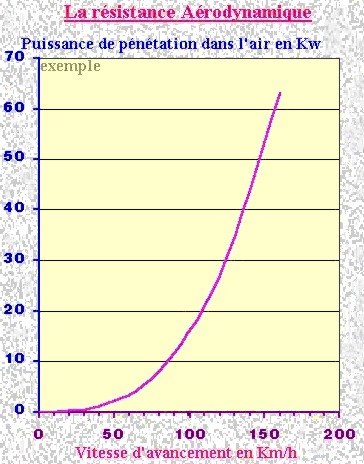
La vitesse de déplacement sur route des engins
agricoles est pour l'instant limitée à 30/40 km/h (en fonction de l'attelage).
Certains pays de la CEE ont autorisé une vitesse
supérieure de 40 et même 50 km/h.
On constate que ces vitesses, relativement réduites,
se situent dans une zone à l'intérieur de laquelle la résistance due à la
pénétration dans l'air peut tout au plus générer une force résistante de
quelques dizaines de décaNewton.
La force due à la résistance de l'air dépend de
nombreux facteurs à savoir:
La section frontale du véhicule (surface du maître
couple en m2)
Le coefficient de résistance au déplacement dans
l'air = 0,3 à 0,6 pour les automobiles
(suivant le modèle) et 0,8 à 1,5 pour les tracteurs
routiers.
La vitesse de déplacement et la vitesse du vent
contraire ont (pour des vitesses élevées)
une très grande influence.
La puissance nécessaire pour vaincre la résistance de
l'air reste faible tant que l'on ne roule pas trop vite, c'est le cas des
engins agricoles.
La force
due à la résistance de l'air se calcule grâce à la formule Suivante:
Fa = 0,5. rP. S.
cx . ( v + v0 )2
Fa = force en
newton due à la résistance
de l'air
r = 1,202
kg/m2 (masse volumique de l'air)
S = section frontale du véhicule
(surface
du maître couple en m2)
cx = coefficient de résistance au
déplacement dans l'air = 0,3 a 0,6 pour les
automobiles (suivant le modèle) et
0,8 a 1,5 pour les tracteurs routiers.
v = vitesse de déplacement en m/s
v0 = vitesse du vent contraire en
m/s