NOM :

INTRODUCTION DES LIAISONS

Auteur P.JOHO

I. Introduction - Vue d'ensemble

Les liaisons mécaniques entre solides sont normalisées internationalement (ISO...), à la fois dans leur désignation (pivot...) et leur représentation schématique. Outils de base, elles sont régulièrement utilisées dans l'étude des systèmes mécaniques.

1. Notion de degré de liberté

Lorsque deux solides sont liés complètement (ou sont en liaison fixe) et qu'il n'y a aucun mouvement relatif possible, on dit qu'ils n'ont aucun degré de liberté ou qu'ils présentent six degrés de liaison.

Inversement, si les deux solides sont totalement indépendants l'un de l'autre, ou n'ont aucun contact, on dit qu'ils présentent six degrés de liberté ou qu'ils n'ont aucun degré de liaison.

Les liaisons usuelles abordées dans ce chapitre sont situées entre ces deux cas extrêmes et présentent des degrés de liberté variant de 1 à 5.

Les six degrés de liberté possibles entre deux solides (il ne peut y en avoir plus) sont trois rotations d'axes perpendiculaires (X, Y et Z) et trois translations suivant ces mêmes axes.

n Exemple de représentation :

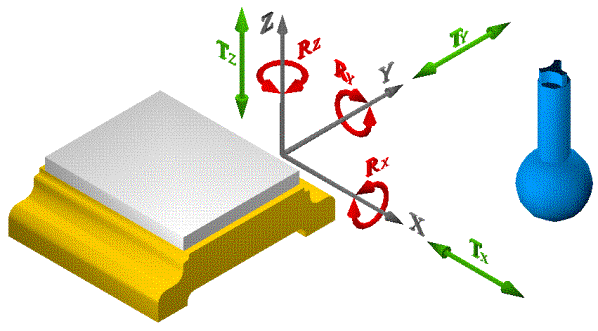
Figure 1

è Remarque : tout mouvement relatif entre solides liés pourra être obtenu par une combinaison plus ou moins complexe de ces six mouvements de base.

Les six degrés de liberté fondamentaux Tableau 1
3 Rotations		3 Translations
Symbole	Désignation	Symbole	Désignation
RX	Rotation d'axe X	TX	Translation suivant X
RY	Rotation d'axe Y	TY	Translation suivant Y
RZ	Rotation d'axe Z	TZ	Translation suivant Z

2. Liaisons mécaniques - Schémas normalisés

Figure 2

3. Liaisons mécaniques - Degrés de liberté des liaisons usuelles

Pour avoir plus de détails concernant une liaison particulière, consulter les paragraphes suivants.

Figure 3

RETOUR SOMMAIRE