Introduction à la simulation numérique

Téléchargez le document de cours ci-dessous
(simnum.pdf)

Généralités :

L’objectif lié à la simulation numérique est multiple. Elle permet entre autre :

de comprendre les phénomènes mis en jeu,

d’aider au dimensionnement,

d’aider au choix technologique, économique, énergétique...,

d'explorer des champs d’investigation que rendrait une approche expérimentale trop longue et coûteuse.

Par rapport à une méthode de résolution traditionnelle (analytique), la simulation numérique est généralement plus rapide et quasiment sans limites quant à la complexité du problème.

Les termes souvent utilisés lors de la mise en œuvre de tels outils sont les suivants :

Modélisation : transformation d’un ou de plusieurs phénomènes physiques, couplés ou indépendants, en expressions (modèles) sensées les représenter. C’est la mise en équation mathématique (généralement différentielle ou aux dérivées partielles) des processus. Elle s’accompagne d’hypothèses, de conditions aux limites (espace) et de conditions initiales (temps).

Discrétisation numérique : Dans la mesure où le choix de la résolution se porte sur une approche numérique, la représentation du ou des phénomènes n’est donc pas continue mais discrète. En d’autres termes, la résolution des équations ne pourra se faire que pour des valeurs définies initialement. Par exemple pour des valeurs de temps et/ou d’espace données. L'écriture du (des) modèle(s) pour chacune de ces valeurs s'appelle la discrétisation.

Résolution numérique et simulation : Pour résoudre ces équations, plusieurs méthodes existent et donnent des résultats plus ou moins fiables et plus ou moins rapides selon la nature du problème. Enfin, l’obtention des résultats est ensuite traitée (généralement graphiquement), pour analyse physique de la réponse au problème posé.

Validation : L'un des avantages du calcul numérique est qu'il donne toujours des résultats. L'un des inconvénients du calcul numérique est qu'il donne toujours des résultats. Aussi, doit-on analyser de façon très critique ce que donne la simulation :

Ai-je pris les bonnes équations (modèles) au départ ?

Suis-je dans les bonnes hypothèses dans lesquelles ces équations sont valides ?

Ai-je pris en compte tous les processus qui interagissent dans mon problème ?

Ai-je bien choisi la méthode de discrétisation ?

Ai-je bien choisi la méthode de résolution ?

Sans compter sur les erreurs d’écriture du programme de calcul ayant permis la résolution.

Il est donc nécessaire de confronter ces résultats avec des étalons pour s’assurer de la validité de son travail. Cette confrontation peut être faite, soit par rapport à un autre modèle, dont la validité n’a pas été mise en défaut, soit par rapport à un montage expérimental, où est réalisé le problème posé et munis de suffisamment de points de mesure pour assurer une comparaison objective.

Néanmoins, si cette comparaison conduit à des écarts acceptables, la simulation effectuée n’en reste pas moins relative à un cas particulier donné initialement. Le modèle ne sera complètement validé que lorsqu'il aura été confronté avec succès avec un nombre suffisant d’étalons.

Dès lors, l’outil créé peut alors servir les objectifs pour lesquels il a été conçu.

Etude de sensibilité paramétrique : le modèle validé peut devenir un outil d’investigation, d’aide au choix... Cette opération consiste à répondre à la question : Que seraient les résultats si au lieu de la valeur X, j’avais Y pour tel paramètre (masse, surface, pression, température) du modèle ?

En conclusion, on part de la physique pour aboutir à la physique, l'association modélisation/discrétisation/résolution ne représentant que l'outil permettant de répondre au problème posé.

Séance n°1 Etude de la répartition axiale des températures dans un échangeur à tubes co-axiaux. Cas de l'échangeur co-courant faisant intervenir deux fluides sans changement de phase en régime permanent.

Hypothèses :

les variables (températures de fluide) sont principalement dépendantes de leurs positions axiales : pas de variation avec l’angle, ni avec le rayon,

Les variations de pression sont négligées,

les variations d’énergie cinétiques et potentielles sont négligées,

Les capacités calorifiques des deux fluides sont constantes au cours de la transformation,

Les échanges thermiques ne sont que d’origine convective,

Les coefficients d’échange convectif sont constants,

L’échange conductif au sein de la paroi est négligé,

L’échangeur est isolé thermiquement de l’extérieur.

Modelisation

La représentation de l’échangeur est la suivante :

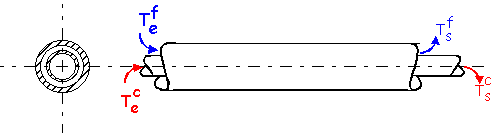
Figure 1 : Représentation schématique de l'échangeur.

L’espace (position axiale) est discrétisé en éléments infinitésimaux de longueur dx. On suppose ensuite que les volumes engendrés par ces éléments sont suffisamment petits pour que la température des deux fluides y soit constante.

Sa représentation est la suivante :

Figure 2 : Séparation de l'échangeur en éléments de volume

La représentation schématique des échanges au sein d’une tranche d’échangeur est la suivante :

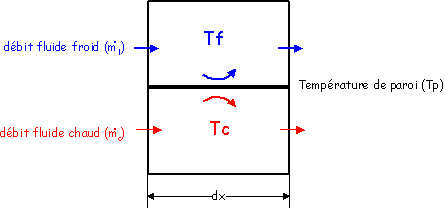
Figure 3 : Tranche élémentaire d'échangeur.

Le premier principe appliqué à l’élément de volume froid de surface d’échange dS_f s’écrit :

l’enthalpie variant de dh au cours de sa traversée du volume, on a : h_s=h_e+dh.

Par ailleurs, on a et dh = Cp_f.dT_f

Le premier principe s’écrit alors :

Avec

K	coefficient d’échange convectif (W/m².K)
dS	Surface d’échange élémentaire (m²)
	Débit massique de fluide (Kg/s)
Cp	Capacité calorifique du fluide (J/Kg.K)
T_f	Température du fluide froid (variable) (°C)
T_c	Température du fluide chaud (variable) (°C)
T_p	Température de paroi (°C)

La même démarche appliquée au fluide chaud conduit à

Pour avoir une relation directe avec x, posons dS=S.dx où S représente la surface linéique (m²/m). De la sorte, l’équation initiale permettra de traiter indifféremment le cas de tubes de sections différentes, avec ou sans ailettes (un tube rond de diamètre D a un S de p D, un tube carré de coté a, un S de 4a,…)

Le système devient alors :

[A]

Cherchons à éliminer T_p de notre expression.

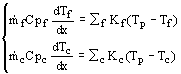Comme il y a conservation de l’énergie (premier principe appliqué au système global), on peut écrire :

[B]

qui ne fait plus intervenir T_p mais bien T_c et T_f ainsi que le facteur

caractérisant l’échange global entre les deux fluides.

Ce flux peut encore s’écrire pour chacun des fluides :

[C]

soit encore

[D]

Exprimons les écarts de température sur chacun des fluides :

[E]

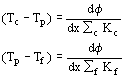En sommant ces deux expressions on obtient :

Par identification avec [B] on a donc :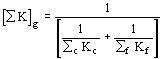

et alors le système devient :

[F]

Arrivé en ce point, la modélisation du système est terminée.

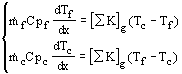Discrétisation

Les deux équations étant du même type, la discrétisation qui suit est valable pour les deux fluides.

La discrétisation dans l’espace s’effectue par exemple en choisissant un pas d’espace constant qui donc implique la connaissance des positions x_i des différents volumes.
représente la dérivée de la fonction T au point x. Sa valeur est par conséquent égale à la pente de la tangente de la courbe T en x.

Dans la mesure où le système est discrétisé en espace, l’accès à la valeur de la dérivée n’est accessible que pour les valeurs x_i.

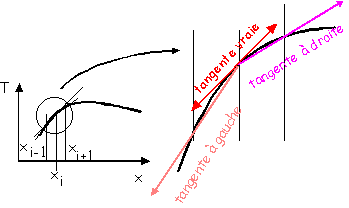
Figure 4 : Signification géométrique des tangentes à gauche et à droite.

La méthode d’Euler consiste à écrire que

On notera que cette écriture ne fait intervenir pour la dérivée calculée en i que des termes en i et i+1 donc à droite du point considéré. On parle alors d’une discrétisation selon un schéma aval. L’utilisation d’un schéma amont (donc à gauche) consiste à écrire :

Une troisième possibilité revient à combiner chacune des deux formulations avec un coefficient pondérateur e :

Lorsque ce dernier est égal à 0.5, on parle alors de schéma centré ou de la méthode de la tangente améliorée.

On remarquera enfin que cette dernière expression permet d’envisager tous les cas précédents :

e=0 : schéma amont,
e=0.5 : schéma centré,
e=1 : schéma aval.

On voit donc que face à un objectif, il existe plusieurs possibilités de l’aborder.

On voit aussi sur le schéma précédent (figure 4), l’origine de l’erreur due à la discrétisation : différence entre dérivée vraie en x (si on était capable de la calculer) et celle calculée après discrétisation (à certaines positions x_i seulement) et que cette erreur est d’autant plus grande que dx est grand.

Bien évidement cette erreur diminue avec dx (augmentation du nombre de points de calcul) puisqu'on tend vers la valeur vraie. Il y a donc un compromis entre la précision que l’on recherche et le temps de calcul directement proportionnel au nombre de points à traiter.

Si on applique à notre cas une discrétisation de type Euler avec un schéma aval, l’équation de départ s’écrit désormais :

Resolution

Puisque le système est axi-symétrique cette équation est valable quelle que soit la valeur de i donc quelle que soit la position du volume dans l’échangeur. Elle l’est donc pour le premier point (x=0, => i=0) qui s’écrit:

[G]

Cette expression fait apparaître les valeurs

qui représentent les températures d’entrée des fluides dans l’échangeur, donc faisant partie des données du problème. L’équation ne fait plus intervenir alors que la seule inconnue

que l’on peut calculer.
La même démarche sur l’autre fluide permet de connaître les deux valeurs de température dans le premier volume (

).
Lorsque cette opération est effectuée maintenant sur le volume n°2, on se retrouve dans le même cas que précédemment (une équation, une inconnue) et on peut ainsi, de proche en proche, calculer le profil de température des deux fluides pour la totalité de l’échangeur.

Devant la simplicité des équations mises en jeu, la résolution numérique est triviale et peut être menée avec un tableur.

Simulation

Les résultats que l’on obtient sont par exemple ceux présentés dans la courbe suivante (figure 5).

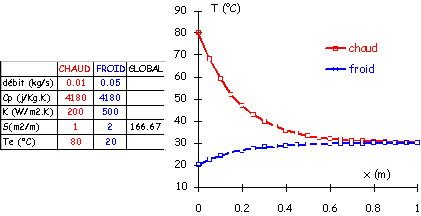
Figure 5: Exemple de résultats de simulation: évolution des températures de fluide.

Dans la mesure où on a calculé la température de chacun des fluides en sortie d’échangeur, on peut donc calculer les puissances mises en jeu par l’échangeur pour chacun des fluides (figure 6) et s'assurer ainsi quelles sont bien égales au cours de leur traversée (vérification modèle).

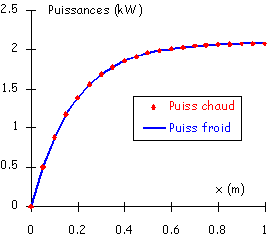
Figure 6: Evolution des puissances échangées au cours de la traversée de l'échangeur.

Un mauvais choix de la valeur de dx peut conduire à des instabilités numériques (dues à une erreur de discrétisation trop importante) qui amène le système à diverger.

Dans les figures qui suivent (7 et 8), pour un même échangeur, la valeur de dx dans le premier cas est de 5 cm (20 points de calcul) et dans le deuxième cas de 2.5 cm (40 points de calcul). Dans la figure 1 le système commence à diverger puis se stabilise alors que dans le second cas, il reste stable tout au long de l’échangeur.

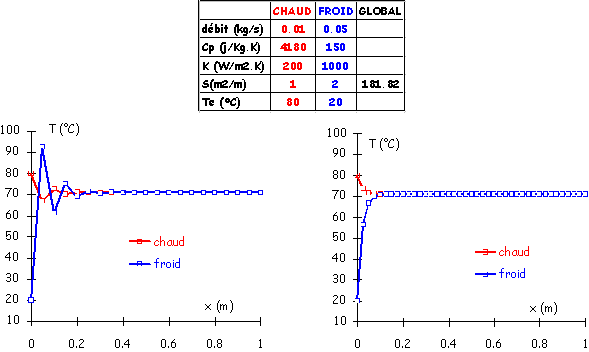
Figure 7 : Illustration de la divergence numérique.

Si on poursuit et que l’on attribue la valeur de 10 cm à dx (10 points de calcul) on obtient alors un système totalement divergent avec des valeurs de température sans aucune signification.

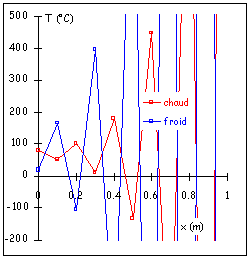
Figure 8 :Système numérique instable, voire chaotique.

Exemple d'étude de sensibilité paramétrique

Il est clair (cf cours Transfert Thermique) que le calcul des coefficients d’échange dépends des conditions d’écoulement (vitesse donc débit, nature du fluide, température, dimensions géométriques de l’échangeur....) et que l’on calcule par le biais des nombres adimensionnels de Reynolds, Prantl et Nusselt.

Néanmoins dans des conditions typiques de production de froid on peut retenir les ordres de grandeurs suivants :

Fluide	Changement de phase (condensation,évaporation)	Eau ou eau glycolée	Gaz (air)
Coefficient d’échange (W/m².K)	Plusieurs milliers	Plusieurs centaines à quelques milliers	Quelques dizaines

Supposons que l’un des fluides soit de l’air (K_c=60 W/m².K). Regardons l’influence de la qualité de l’échange de l’autre fluide sur le comportement de l’échangeur. On obtient les résultats suivants pour des valeurs de 250, 1000 et 2000 W/m².K concernant K_f

Figure 9 :Etude de la sensibilité paramétrique du coefficient d'échange le plus grand

On voit au travers de cet exemple que si l’on veut augmenter les performances de l’échangeur, il est inutile d’agir sur le fluide possédant les meilleures qualités de transfert.

Dans la mesure où le coefficient d’échange intervient toujours en facteur de la surface dans les équations, il est par conséquent inutile de chercher à augmenter celle du coté du fluide qui possède les propriétés de transfert les plus intéressantes. En revanche cela montre qu’il faut au contraire privilégier l’autre fluide. C’est la raison pour laquelle, quand un échangeur fait intervenir de l’air comme fluide, c’est toujours ce côté qui est muni d’ailettes (radiateur sur une voiture, aéroréfrigérant,...)

Toujours avec le même exemple (K_c=60 W/m².K) et en prenant une valeur de 1000 W/m².K pour K_f, supposons que l’adjonction d’ailettes multiplie par un facteur 10 la surface offerte à l’air, la comparaison prend alors la forme suivante :

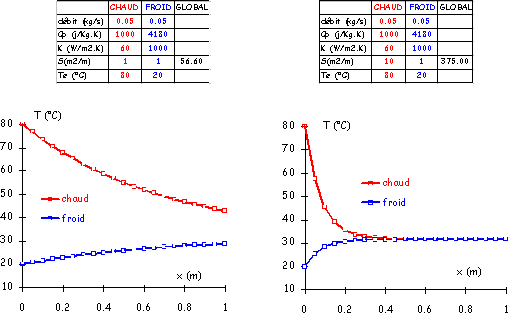
On pourrait comme cela multiplier les enseignements que l’on pourrait tirer de l’outil qui a été créé.

Voici par exemple quelques idées pour compléter ce travail :

Intégrer dans le modèle le calcul des coefficients d’échange en fonction du débit et de votre type de veine fluide,
Prendre en compte les transferts de chaleur de l’échangeur avec l’ambiance
Prendre en compte le transfert thermique dans la paroi d’échange,
Simuler un échangeur fonctionnant à contre courant,
Simuler un échangeur où interviennent à la suite différentes conditions d’écoulement (désurchauffe, condensation et sous-refroidissement) dans un condenseur par exemple.
...

Téléchargez la feuille de calcul de la séance 1

(echangeur.xls)